EP10: O preço dos ativos e a distribuição log-normal
Entenda porque o preço de alguns ativos em renda variável segue a distribuição log-normal e porque as penny stocks são as preferidas de alguns investidores.
Introdução
Este artigo é apenas instrutivo, não tendo qualquer recomendação de investimentos.
Consulte um profissional certificado CNPI para obter orientação sobre onde investir.
Desta vez gostaria de escrever sobre o preço das ações e discutir porque elas seguem uma distribuição log-normal e não a normal, como muitos podem acreditar. Antes de irmos em frente, vamos conhecer essas duas distribuições estatísticas:
O que é uma distribuição normal
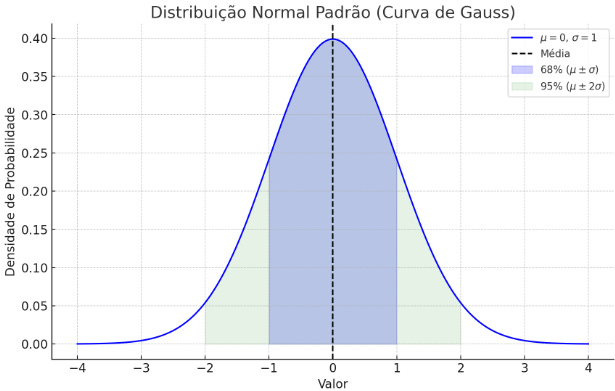
A distribuição normal também é chamada de distribuição gaussiana, curva de Gauss ou Curva de Sino é um dos conceitos mais importantes da estatística e da probabilidade. Ela descreve como os dados se distribuem em torno de uma média, assumindo um padrão simétrico em forma de sino.
Características principais:
Simetria:
A curva é simétrica em torno da média. Quer dizer que metade dos dados fica à esquerda da média e a outra metade à direita.Média = Mediana = Moda:
Sendo uma distribuição é simétrica, os três valores coincidem com o centro da curva.Formato de sino:
A maioria dos valores está próxima da média, e a frequência diminui conforme os valores se afastam dela (para mais ou para menos). Por exemplo, a média de altura das brasileiras é de aproximadamente 1,60m1 e a maior parte delas estão ao redor da média. É muito difícil encontrar uma brasileira com 1,30m assim como encontrar uma de 1,90m.Desvio padrão:
O desvio padrão (σ) determina a largura da curva e qual a probabilidade de um dado elemento se desviar da média.Aproximadamente 68% dos dados estão entre μ−σ e μ+σ
Aproximadamente 95% estão entre μ−2σ e μ+2σ
Aproximadamente 99,7% estão entre μ−3σ e μ+3σ
No caso das mulheres brasileiras, o desvio padrão é de 6,5 cm, ou seja, a probabilidade de encontrar uma mulher de 1,54 até 1,67 é de aproximadamente 68%.
Representação matemática da função densidade da distribuição normal:
Onde:
μ = média
σ = desvio padrão
e = número de Euler (~2,718)
x = valor da distribuição
Reparem que em nosso último artigo falamos sobre o “Número Mágico”, que é o número de Euler. Caso não tenha visto ainda, convido para que leia, pois ajudará a entender melhor este artigo aqui:
Aplicações da distribuição normal:
Estatística inferencial: testes de hipóteses, intervalos de confiança;
Psicologia e educação: QI, notas de prova: a maior parte das pessoas tem um QI ao redor de 100, com um número menor de indivíduos pouco inteligentes ou excepcionais;
Ergonomia: o exemplo que citei acima sobre a altura das brasileiras é um dado que pode ser modelado pela distribuição normal;
Controle de qualidade: análise de variabilidade em processos industriais. Numa fábrica, o peso de um produto deve ser aproximado para todas as embalagens produzidas, com uma margem de erro para baixo ou para cima (desvio);
O que é uma distribuição log-normal
Agora que já temos informações sobre o que é uma distribuição normal, vamos entender o que é uma distribuição log-normal pelas diferenças com a anterior. Esta é uma distribuição onde os elementos aparecem com maior frequência no começo da curva e possui uma cauda longa. Essa distribuição representa algumas situações no nosso mundo real, como por exemplo:
Internações em hospitais: espera-se que um paciente não fique muitos dias internado. São raros os doentes que passam muitos anos no hospital e a maioria volta para casa depois de algum tempo;
Renda da População: os indivíduos mais ricos são pouco numerosos, representam a minoria na sociedade;
Tamanho das Empresas: a maior parte das empresas são micro e pequenas. As empresas de grande porte são pouco numerosas.
O preço das ações no mercado financeiro também segue essa distribuição. A Maior parte dos ativos tem preços que giram em torno de uma média, com poucas ações custando pouco (penny stocks) e ainda menos ações custando muito. São poucas empresas com preços acima de R$ 60 nos dias de hoje (15/05/2025). Mais raras ainda são empresas com ações acima de R$ 200, praticamente dez ativos listados2.
A distribuição log-normal não tem média e desvio padrão como a distribuição normal. Ela tem dois conceitos semelhantes: local (location) e escala, tal que:
local = média (ln(xi))
escala = desvio padrão (ln(xi))
Outra característica importante na log-normal é que não existem números Xi negativos (Xi > 0). Você já viu alguma ação com preço negativo? Pois é… O mínimo que o preço pode chegar numa falência de S/A é a zero, o que reforça a aderência nesta distribuição.
Convertendo dados de uma distribuição normal para log-normal e vice-versa
Os dados de uma distribuição log-normal podem ser convertidos numa distribuição normal da seguinte forma:
De normal (Xi) para log-normal (Xn):
De log-normal (Xn) para normal (Xi):
Para converter dados de uma distribuição log-normal para uma distribuição normal, aplica-se o logaritmo natural aos dados. Se os dados originais (Xn) seguem uma distribuição log-normal, então os seus logaritmos naturais seguem uma distribuição normal.
Por que o preço das ações seguem a distribuição log-normal e não a normal?
Agora que conhecemos as características das duas distribuições, fica mais simples de entender como os preços seguem a distribuição log-normal.
O que podemos inferir:
Os preços tem uma tendência maior de subirem do que de caírem;
Não existem preços negativos de ações (característica da curva normal);
As mudanças diárias no preço das ações (variações), diferente dos preços em si, seguem uma distribuição normal;
Existem poucas penny stocks na B3: na data de hoje, por volta de 20 papéis;
A maior parte das ações estão na faixa de R$ 27 a R$ 60;
Existem ações acima de R$ 60, menos numerosas;
As ações acima de R$ 125 são raras;
O motivo do preço ser log-normal se deve em grande parte à capitalização (compounding). Suponha uma ação com o preço de R$ 100:
Ela sobe 10% no primeiro dia e cai 10% no dia seguinte. É comum imaginar que volte a R$ 100, mas isso não ocorre pelo seguinte:
D1 (+10%): 100 + 100 x 0,10 = R$ 110
D2 (-10%): 110 - 110 x 0,10 = R$ 99
Note que nessas duas movimentações ocorre uma perda de 1% no preço: 1,10 x 0,9 = 0,99.
Vamos considerar a seguinte escala:
Repare que se a ação subir quatro dias seguidos, ela aprecia 8,24%.
Por outro lado, se uma ação cai 4 dias seguidos, deprecia só 7,76%.
Isso ocorre por causa do efeito de capitalização (compounding). Quanto maior a taxa de capitalização, mais dramático é o evento. Vamos supor que essa mesma taxa de 2% suba para 5% ou 10%.
Para uma capitalização de 10%, note que uma ação que sobe 4 dias seguidos atinge um aumento de 46,41%, frente a 21,55% na capitalização de 5%.
Nessa mesma capitalização de 10%, a perda também é muito maior, de -34,39% face a -18,55% capitalizando em 5%.
O preço de uma ação também afeta a forma como as cotações se desenvolvem. Consideremos duas ações: uma de R$ 3,83, como é o caso da KLBN4 (Klabin Preferencial) e outra de R$ 52,95 que é a UNIP6 (Unipar Preferencial). Se ambas as ações subirem R$ 1,00 ou caírem em dias consecutivos:
Note como uma variação de R$ 1,00 nas duas ações produzem valorizações diferentes em cada caso. Na KLBN4, um aumento de R$ 1,00 produz, em quatro dias seguidos, mais de 104% de crescimento. No segundo caso, produz apenas 7,55% de variação em UNIP6.
Existem investidores que gostam de penny stocks ou ações de preços baixos. A demonstração anterior pode mostrar como uma ação de preço baixo, de uma empresa bem escolhida, com potencial de crescimento, é capaz de gerar uma valorização explosiva.
O preço sozinho significa pouca coisa
Se as ações custam pouco, existem seus motivos…
A base acionária da empresa pode ser grande demais: numa pizza muito dividida, quem tem só uma fatia passa fome. É necessário possuir muitas fatias (shares) para deter uma parte relevante do capital social ou receber bons dividendos - o DPA (Dividendo por Ação) é calculado dividindo o valor total da distribuição (pizza) pelo número total de ações em circulação (número de fatias);
Estratégia de liquidez: é mais acessível ao pequeno investidor comprar uma ação de uma Companhia de R$ 3,50 do que uma de R$ 55,80. Mas já vimos que a fração do negócio que o investidor está levando também é menor, já que existem mais sócios. Uma única ação da Berkshire Hathaway classe A chega recentemente a custar US$ 760 mil, pois a empresa tem uma estratégia de recompra de ações, retirando cada vez mais sócios do negócio. Quanto maior o preço, menor a liquidez e mais difícil de montar ou desmontar uma posição na carteira;
Estratégias de Financiamento: bancos vivem expandindo a sua base acionária por questões de Basileia, pois precisam aumentar o seu capital próprio para conseguirem emprestar ainda mais dinheiro. Empresas em fase de expansão podem pagar a aquisição de outros negócios com ações próprias… Existem muitas estratégias de financiamento por meio de capital próprio (ke) que afetam o preço das ações;
Conjuntura Econômica e Qualidade dos Negócios: por fim, uma parte considerável da ações que custam pouco são negócios passando por dificuldades, em turnaround ou realmente ruins, sendo evitados pelos investidores.
Este artigo é apenas instrutivo, não tendo qualquer recomendação de investimentos.
Consulte um profissional certificado CNPI para obter orientação sobre onde investir.
Para muitos investidores experientes, o motivo de buscar ações baratas é para conseguir colecionar uma grande quantidade delas na expectativa de que os negócios cresçam, gerando ganho de capital ou ainda bons dividendos.
Cabe a cada um conhecer os negócios, entender a mecânica dos preços e calcular o preço justo dos ativos para decidir como e onde investir.
Resumindo dos principais pontos:
O preço sozinho significa pouca coisa e só começa a fazer algum sentido ao conhecer o negócio (tamanho da base acionária, estratégia, demonstrações financeiras etc);
O mercado precifica os ativos de forma razoavelmente eficiente, porém o preço nem sempre está de acordo com o valor intrínseco do negócio;
Nem sempre é tão simples de saber que um negócio está descontado ou majorado;
Resumo do Resumo:
Se você não é capaz de saber o preço justo de um ativo, se está descontado ou majorado, então nem deveria começar a operar esse ativo.
É só comprar e esperar?
A coisa não é tão simples quanto parece, pois as duas empresas tem bons fundamentos e são ativos de qualidade. No entanto, cada setor ou negócio tem características e capitalização peculiares. Vamos analisar KLBN4 desde 01/01/2015. Os dados são cortesia do Yahoo! Finance:
Repare que o preço da ação variou pouco num período de 10 anos. De R$ 2,50 a R$ 5,50, ou pouco mais do que o dobro (120%).
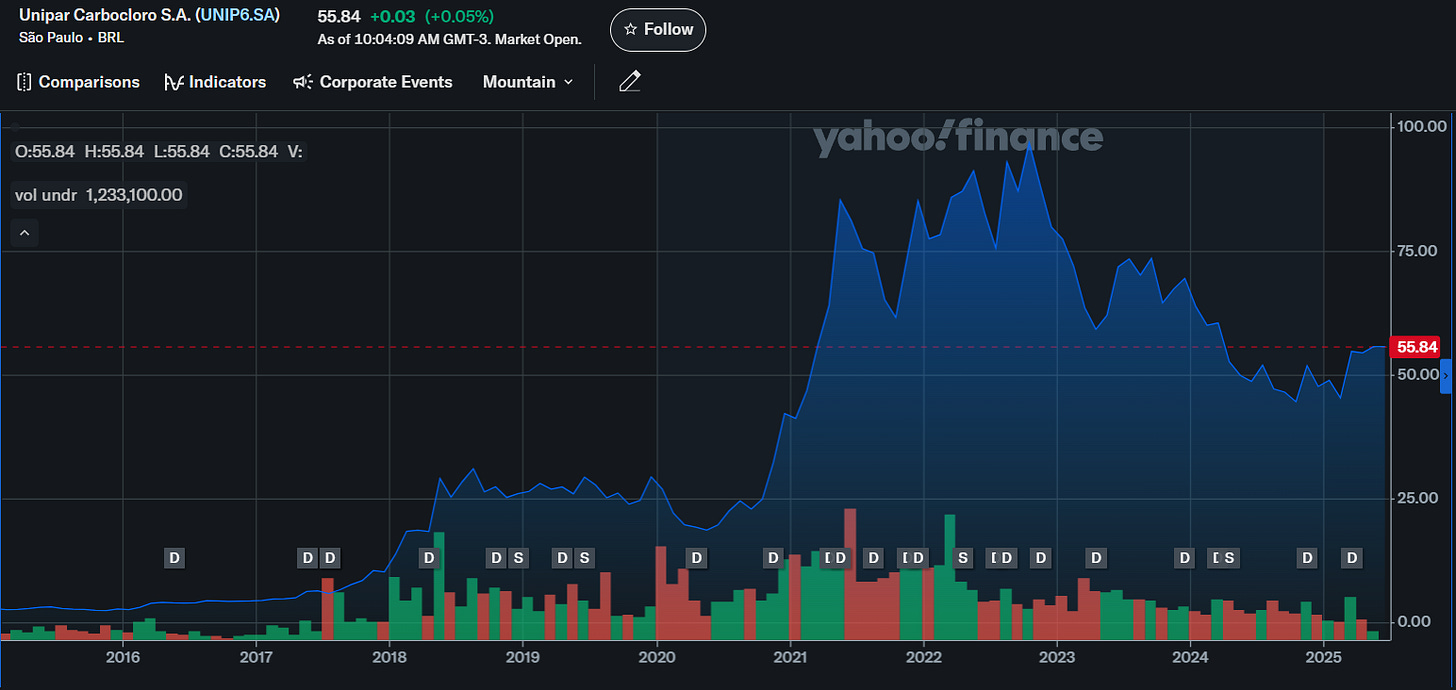
Vamos analisar agora a UNIP6, uma small cap, nessa mesma janela de tempo:
Ela custava por volta de R$ 3,00 em 2015 e ficou neste patamar por vários anos. Em seguida foi subindo até atingir picos de quase R$ 100,00. Atualmente está em R$ 55,84. Mesmo nesse patamar mais baixo, o ganho de capital foi de 1.760% em 10 anos.
Um investidor que tem uma carteira com os dois ativos, teria sido melhor sucedido se tivesse comprado UNIP6 em 2015 e KLBN4 da metade de 2016 até meados de 2019. Em ambos os casos, teria de conhecer a qualidade dos negócios, entender o preço justo dos ativos e reconhecer quando estavam descontados. Mais ainda: teria de ter recursos naquela ocasião e estômago para investir num momento em que todo o mundo estava vendendo. É simples analisar o passado e muito complicado operar desse modo porque as capacidades exigidas desse investidor são pelo menos três:
Capital disponível: não adianta nada ter as outras duas capacidades, um bom temperamento e conhecimento que um ativo está descontado, mas não ter dinheiro para investir na hora que uma oportunidade aparece;
Conhecimento Técnico: volte e leia novamente o Resumo do Resumo. As pessoas são capazes de identificar um produto caro num supermercado e preços baixos no cotidiano, para um móvel ou TV. Elas passam um longo tempo pesquisando o melhor preço… Mas raramente são capazes de calcular o preço justo de um ativo financeiro, erro que pode gerar muita frustração e perdas financeiras.
Temperamento: o investidor pode ter dinheiro e identificar uma oportunidade, mas ser influenciado por vários vieses cognitivos ou sucumbir ao medo. Num momento como esse, operando de forma contrária: vendendo quando deveria comprar, vendendo quando deveria manter e assim por diante…
Essas três capacidades são temas futuros e voltaremos neles em várias ocasiões. Falamos muito do preço de ações, mas pouco de derivativos. É outro assunto longo, que merece vários artigos. Neste aqui vamos tocar só num ponto relacionado com a log-normal:
Por que o modelo Black&Scholes usa a distribuição normal em vez da log-normal?
Muitas pessoas afirmam que existe uma limitação no modelo por esse motivo. Será que isso é mesmo verdade?
Quem tiver curiosidade na fórmula de B&S. Você encontrará um logaritmo natural (ln) num de seus componentes (d1):
Onde:
C = preço da opção de compra (call)
S0 = preço atual da ação
K = preço de exercício (strike)
T = tempo até o vencimento (em anos)
r = taxa de juros livre de risco (contínua)
σ = volatilidade do ativo subjacente (desvio padrão anual dos retornos logarítmicos)
N(di) = função de distribuição acumulada da normal padrão (probabilidade de que uma variável aleatória normal padrão seja menor que di)
Vimos até aqui que o preço das ações é log-normal e o logaritmo neperiano (ln) das variações nos preços das ações é normal.
O cálculo da Função de Distribuição Acumulada Normal Padrão usa o componente d1, que por sua vez tem um logaritmo natural para transformar a variação do preço, logo há uma conversão para a distribuição normal. O modelo pode ter as suas limitações, mas não por esse motivo.
Espero ter ajudado você a entender um pouco mais a dinâmica de preços dos ativos… Mas o preço é apenas um dos fatores analisados por um investidor. Nunca deixe de avaliar a qualidade dos negócios e buscar um profissional qualificado sempre que necessário. Até a próxima!
https://www2.anac.gov.br/arquivos/pdf/Relatorio_Final_Projeto_Conhecer.pdf
https://www.b3.com.br/pt_br/market-data-e-indices/servicos-de-dados/market-data/