EP9: Capitalização Contínua e o Número Mágico
Entenda as diferenças entre a Capitalização Discreta, Contínua e conheça um número mágico...
Introdução
Aproveitando que a Taxa Selic subiu nesta semana, gostaria de escrever esse artigo sobre taxas e capitalização. A Taxa real é diferente da Taxa Nominal. Considere uma Taxa Nominal de 12% ao ano, capitalizada mensalmente. Essa taxa equivale a uma Taxa Nominal mensal de 1% ao mês. Porém se acumularmos essa taxa, temos uma taxa real/efetiva de 12,68% ao ano:
(1+0,01)^12 = 0,1268
Os banqueiros logo perceberam que quanto menor o período de capitalização, maior era o ganho que tinham nos empréstimos. Se capitalizar por dia, hora, minuto ou mesmo por segundo, perceberá que existe um limite para o qual se chega num “número mágico”. Vamos capitalizar por dia:
n = número de capitalizações.
i = taxa de juros.
Vamos gerar um gráfico:
n = 1: f(1) = (1 + 12% / 1) ^ 1 - 1 = 12,0%
n = 2: f(2) = (1 + 12% / 2) ^ 2 - 1 = 12,36%
n = 3: f(3) = (1 + 12% / 3) ^ 3 - 1 = 12,48%
n = 4: f(4) = (1 + 12% / 4) ^ 4 - 1 = 12,55%
n = 5: f(5) = (1 + 12% / 5) ^ 5 - 1 = 12,58%
…
n = 50: f(50) = (1 + 12% / 50) ^ 50 - 1 = 12,73%
…
n = 365: f(365) = (1 + 12% / 365) ^ 365 - 1 = 12,74%
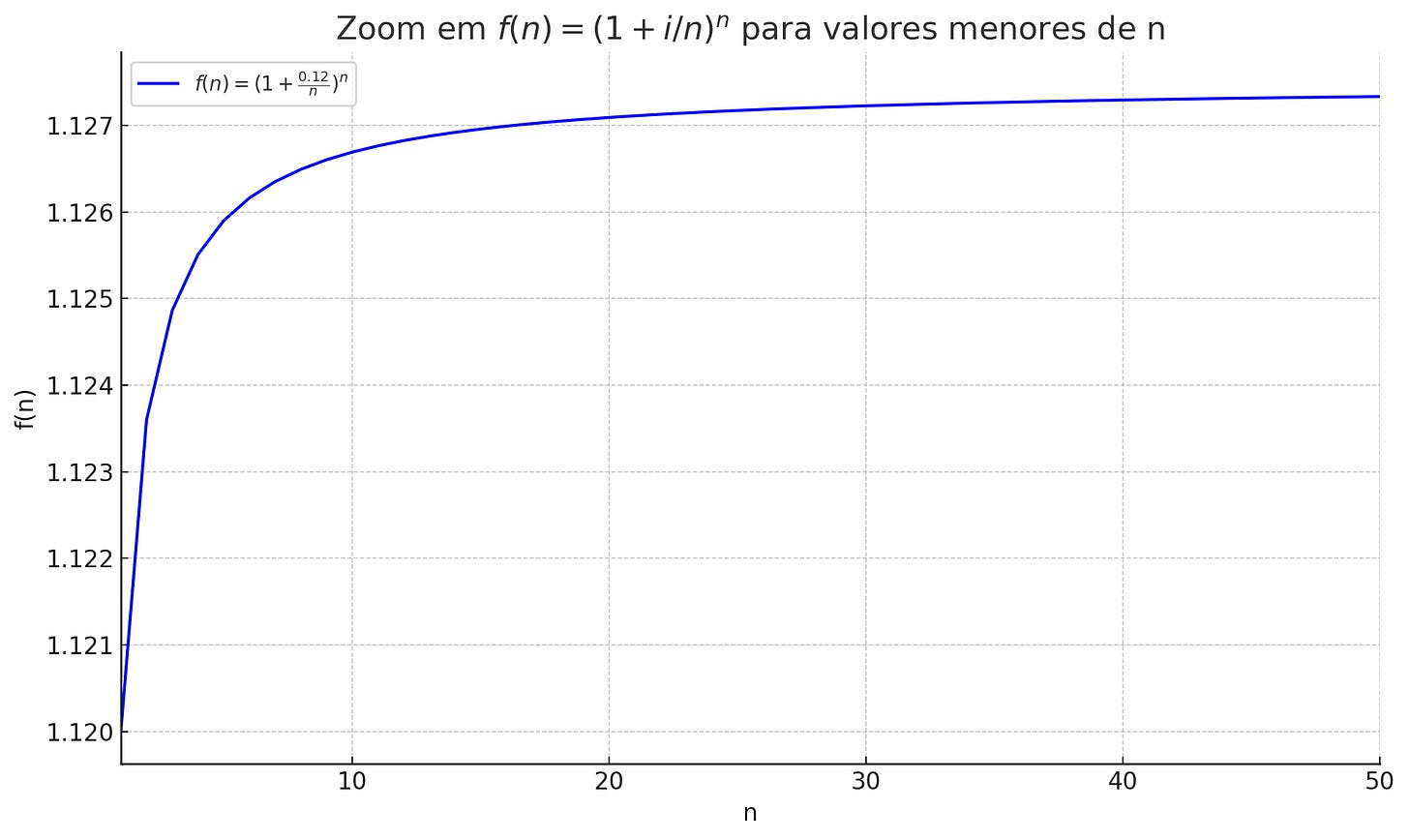
Aqui está o gráfico desta função:
Trata-se de uma função exponencial. Vamos ampliar o gráfico entre os dias 1 e 50 para termos uma visão melhor dela.
O limite desta função, quando o n tende ao infinito é o “número mágico”, o número de Euler elevado à taxa de juros:
O número de Euler, representado pela letra e é uma constante matemática infinita, assim como o pi, com valor aproximado de 2,7182818284. Ele é a base dos logaritmos neperianos e tem muitas aplicações em finanças, pois sua exponenciação é capaz de representar uma taxa de juro aproximada. Portanto, se você quiser calcular um investimento futuro com ele, pode realizar da seguinte forma:
Onde:
C = Montante final
C0 = Capital Inicial
i = taxa de juros
e = número de Euler: 2,7182818284
n = número de períodos de capitalização
Outra forma de entender a equação acima é substituir o número de Euler:
Cálculo da capitalização contínua
Suponha que temos R$ 1000 e queremos saber o valor do nosso investimento com capitalização contínua a uma taxa selic de hoje (14,75%) por um período de 3 anos:
C = R$ 1000 x 2.7182818284 ^ (0,1475 x 3)
C = R$ 1.556,60
Cálculo com capitalização discreta
Juros compostos são “juros sobre juros”, ou seja, os juros são reaplicados a cada intervalo de tempo, um após o outro.
A fórmula é:
Onde:
C = Montante
C0 = Capital Inicial
i = taxa de juros
n = número de períodos de capitalização
O Montante permanece sendo também o Capital Inicial mais os Juros:
Calculamos o valor futuro dos mesmos R$ 1.000, capitalizados anualmente à taxa de 14,75% a.a. durante 3 anos, usando juros compostos.
C0 = R$ 1000
i = 0,1475
n = 3
Substituindo:
C=1000 x (1 + 0,1475) ^ 3 = aproximadamente R$ 1.511
Você pode fazer essa conta com a HP-12C também:
PMT = 0
PV = -1000
i = 14,75
n = 3
FV = 1.510,97
Capitalização Discreta x Contínua
Uma dúvida que pode ocorrer para muitos é a seguinte:
Por que a Capitalização Anual e a Contínua geram valores futuros diferentes, com a mesma taxa de juros, tempo de capitalização e capital inicial?
Os valores futuros não são iguais, e a diferença entre eles é justamente a forma de capitalização.
Capitalização anual (discreta ou periódica): os juros são aplicados apenas uma vez por ano, ao final de cada período.
Capitalização contínua: os juros são aplicados de forma ininterrupta, a todo instante, como se fossem reinvestidos continuamente.
Isso quer dizer que a capitalização contínua gera um montante maior do que a capitalização anual para a mesma taxa e período, porque o dinheiro "trabalha" o tempo todo — é a forma mais intensiva de aplicação de juros compostos. O gráfico a seguir mostra a diferença entre as duas ao longo do tempo.
Quanto maior o tempo, mais acentuada essa diferença se torna. Repare que ao final de 25 anos, a diferença entre as duas é de quase R$ 10.000.
Para juros discretos, uma perda de -14,75% não é compensada por um ganho de +14,75%. Mas uma perda de e ^ (-0,1475) + e ^(0,1475) são compensados perfeitamente. Falaremos mais sobre as penny stocks no próximo artigo e porque a variação delas é mais acentuada que as demais. Esse artigo é uma base para o assunto que será tratado em breve.
Casos de Uso
A taxa de capitalização contínua é comumente usada em várias áreas onde os investimentos e os cálculos financeiros envolvem uma aplicação contínua de juros. Ela é especialmente relevante em situações onde o tempo e a frequência com que os juros são aplicados têm grande importância. Aqui estão alguns casos onde ela costuma ser aplicada:
1. Mercados Financeiros e Investimentos
Títulos e ações: No mercado de títulos de longo prazo ou ações, a capitalização contínua é muitas vezes usada para calcular os rendimentos de uma obrigação ou ações ao longo do tempo. Ela assume que os juros ou retornos podem ser acumulados constantemente;
Opções financeiras e derivativos: No caso de derivativos, como opções, é comum usar capitalização contínua para precificar ativos financeiros e calcular o valor de opções, pois esses mercados muitas vezes lidam com eventos que podem mudar o panorama do mercado a qualquer momento (e não de forma periódica).
2. Modelos de Crescimento e Decaimento
Modelos de crescimento populacional: A fórmula de crescimento contínuo é usada para modelar a expansão populacional ou o crescimento de bactérias, por exemplo, onde o aumento ocorre de forma constante e contínua.
Decaimento radioativo: O modelo de decaimento de substâncias radioativas também segue uma taxa de capitalização contínua, onde a desintegração de partículas acontece de maneira constante ao longo do tempo.
3. Contabilidade e Finanças Corporativas
Cálculos de juros compostos: Para empresas e bancos que oferecem investimentos de juros compostos, a capitalização contínua é utilizada em alguns cálculos financeiros mais avançados, especialmente em modelos de otimização financeira.
4. Economia
Modelos de crescimento econômico: No campo da economia, a capitalização contínua é utilizada em modelos de crescimento econômico, onde as variáveis (como produção ou consumo) aumentam continuamente, sem intervalos de tempo fixos.
5. Ciências Atuariais e Seguros
Em algumas práticas atuariais, a capitalização contínua é usada para avaliar seguros e pensões, já que os fluxos de caixa (pagamentos de prêmios e benefícios) podem ser considerados de forma contínua em vez de periódica.
Vantagens de usar a capitalização contínua:
Preciso e realista: É uma abordagem mais realista para modelar situações onde o tempo de acumulação é contínuo e sem interrupções.
Simplicidade matemática: As fórmulas e os cálculos se tornam mais simples ao utilizar a constante de Euler (e), especialmente quando lidamos com processos de crescimento exponencial.
Espero que você tenha gostado de entender as diferenças entre a Capitalização Discreta e Contínua. Fique sempre de olho no regime de capitalização dos juros dos seus contratos, investimentos e dívidas!