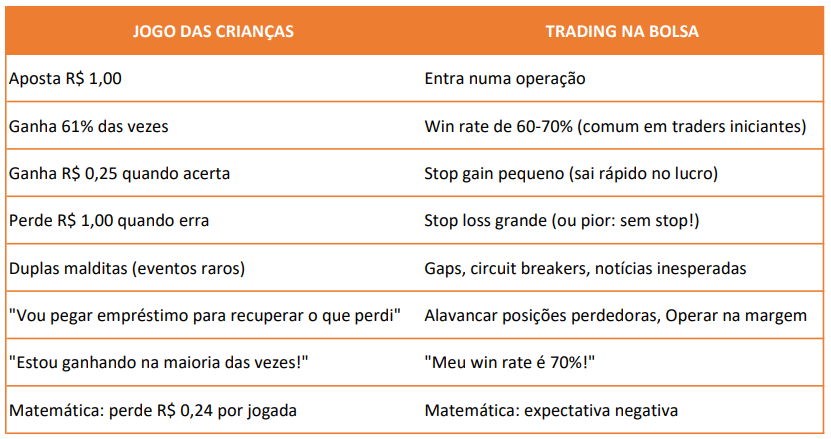
EP15: A Lógica do Trading

Um jogo simples, dois dados e um resultado inevitável: entenda como mesmo ganhando na maioria das vezes, quase todos quebram.

Atenção: o jogo "Prejuízo Premiado" é apresentado para fins didáticos e ilustrativos. Não deve ser usado com dinheiro real, nem para auferir lucros de qualquer espécie. O Autor deste artigo se isenta de qualquer responsabilidade por seu uso.

Introdução

Entrei numa sala de aula para ensinar matemática em 1994, com 19 anos, para três classes do ensino médio. Foi uma passagem breve mas bastante divertida, de apenas seis meses, quando substituí a professora titular, que estava de licença médica:

- “Imagine que você tem um molho com cinco chaves e precisa abrir uma porta. Você não sabe qual é a chave correta e vai precisar testar uma por uma. Qual é a probabilidade de você acertar a chave na primeira tentativa? - A probabilidade é de 20% porque você tem apenas uma chave correta entre cinco disponíveis. Essa probabilidade vai aumentando conforme você tenta as próximas. Na segunda tentativa, a probabilidade aumenta para 25%, porque agora você tem uma chave em quatro…”

- “Está errado, professor!” - interrompeu uma aluna.

- “Tudo bem, então explique o que você está pensando…” - respondi e pedi para mostrar a sua linha de raciocínio.

- “É simples… Se você tem uma chave, ou ela abre a porta ou não, então a probabilidade de acertar a chave é de 50%” - ela me corrigiu.

Pensei comigo: “essa garota podia jogar todos os dias na mega-sena, pois ganharia pelo menos um dos três sorteios toda a semana…”.

Probabilidade é assim mesmo… Nunca é um assunto intuitivo e as pessoas podem levar anos para dominá-lo.

Algumas aulas eram tristes, pois a maioria dos alunos não gostava do assunto. Outras eram mais engraçadas… Como sempre, gostei de criar jogos, então preparei um para mostrar como funcionava um cassino simplificado. Não queria trazer um baralho nem uma roleta para a classe — e pensar que hoje tem aluno trazendo até revólver para a aula… Enfim… Trouxe um par de dados no bolso, um pote de moedas e ficamos duas aulas seguidas (dobradinha) jogando.

Esses dias estava desocupando a minha casa antiga para alugar e encontrei as regras desse jogo que escrevi. Se você quiser experimentar com seus amigos, leia o disclaimer no início deste artigo. Use com os seus filhos, pois será bem divertido e educativo para eles:

Jogo “Prejuízo Premiado”

Componentes (5 participantes)

1. Dois dados de seis faces

2. Pote com moedas:

   1. 50 moedas de R$ 1,00

   2. 10 moedas de R$ 0,25

3. Papel e caneta, para anotar os empréstimos das crianças

Regras do Jogo

1. Preço da aposta R$ 1,00

2. Coloque sua moeda na mesa

3. Role os dois dados

4. Veja o resultado:

   1. SE SAIR DUPLAS (1-1, 2-2, 3-3, 4-4, 5-5 ou 6-6):

      1. DUPLAS MALDITAS!

      2. A BANCA GANHA

      3. Sua moeda vai para a lata da banca

      4. Você perde o que apostou

   2. SE A SOMA FOR 8 OU MENOS (sem ser duplo):

      1. Você GANHOU!

      2. Recebe a sua moeda de volta

      3. Ganha mais R$ 0,25 da banca

      4. Total: você recebe R$ 1,25

   3. SE A SOMA FOR 9 OU MAIS (sem ser duplo):

      1. A banca GANHOU!

      2. Sua moeda vai para a lata da banca

      3. Você perde o que apostou

5. Você pode começar o jogo com R$ 5,00 (5 moedas de R$ 1,00)

6. Você pode emprestar da banca uma única vez, mais R$ 5,00. Na segunda você está falido(a) e sai do jogo.

Organizei a classe em grupos de cinco jogadores e, juntos, realizamos de dez a vinte rodadas para cada grupo. Fomos usando a lousa para controlar o dinheiro distribuído e os empréstimos concedidos. Ainda tenho as anotações dos resultados dos jogos.

Na metade da segunda aula, a maior parte dos alunos já estava quebrada e devendo à banca.

Na aula seguinte, dois dias depois, expliquei o funcionamento do jogo à turma.

Dissecando o Jogo

Calculando todas as combinações possíveis

Com 2 dados, temos 6 × 6 = 36 combinações válidas e equiprováveis:

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

Identificando as duplas

Duplas (BANCA GANHA automaticamente):

• (1,1), (2,2), (3,3), (4,4), (5,5), (6,6)

• Total: 6 combinações

• Probabilidade: 6/36 = 1/6 ≈ 16,67%

Cálculo das somas (sem duplas)

02: 0 combinações (1,1) é uma dupla removida;
03: 2 combinações (1,2); (2,1);
04: 2 combinações (1,3); (3,1) - remove dupla (2,2);
05: 4 combinações (1,4), (4,1), (2,3), (3,2);
06: 4 combinações (1,5), (5,1), (2,4), (4,2) - removida dupla (3,3);
07: 6 combinações (1,6), (6,1), (2,5), (5,2), (3,4), (4,3);
08: 4 combinações (2,6), (6,2), (3,5), (5,3) - removida dupla (4,4);
09: 4 combinações (3,6), (6,3), (4,5), (5,4);
10: 2 combinações (4,6), (6,4) - removida dupla (5,5);
11: 2 combinações (5,6), (6,5);
12: 0 combinações (o único era 6+6, que é dupla);

Contando os resultados

Jovem ganha (soma <= 8, sem duplos):

• Soma 3: 2 combinações;

• Soma 4: 2 combinações;

• Soma 5: 4 combinações;

• Soma 6: 4 combinações;

• Soma 7: 6 combinações;

• Soma 8: 4 combinações;

• 2 + 2 + 4 + 4 + 6 + 4 = 22 combinações;

• Probabilidade de 22 / 36 ou 61,11%

BANCA GANHA (duplos ou soma >= 9):

• Duplos: 6 combinações;

• Soma 9: 4 combinações;

• Soma 10: 2 combinações;

• Soma 11: 2 combinações;

• 6 + 4 + 2 + 2 = 14 combinações;

• Probabilidade de 14 / 36 ou 38,89%

Resultado por Jogada

Quando o(a) Jovem ganha (22 / 36 das vezes):

• Apostou: R$ 1,00

• Recebeu: R$ 1,25

• Lucro líquido: R$ 0,25

Quando a Banca ganha (14 / 36 das vezes):

• Recebeu: R$ 1,00

• Lucro líquido: R$ 1,00

Expectativa

A expectativa matemática é a média do que você ganha ou perde por jogada no longo prazo.

Fórmula:

E(X) = P(ganhar) × Lucro(ganhar) + P(perder) × Lucro(perder)

Cálculo:

E(X) = (22/36) × (0,25) + (14/36) × (-1,00)

E(X) = 22 × 0,25 / 36 + 14 × (-1,00) / 36

E(X) = 5,50/36 - 14,00/36

E(X) = -8,50/36

E(X) = -0,2361...

E(X) ≈ -R$ 0,24 por jogada

Mecânica

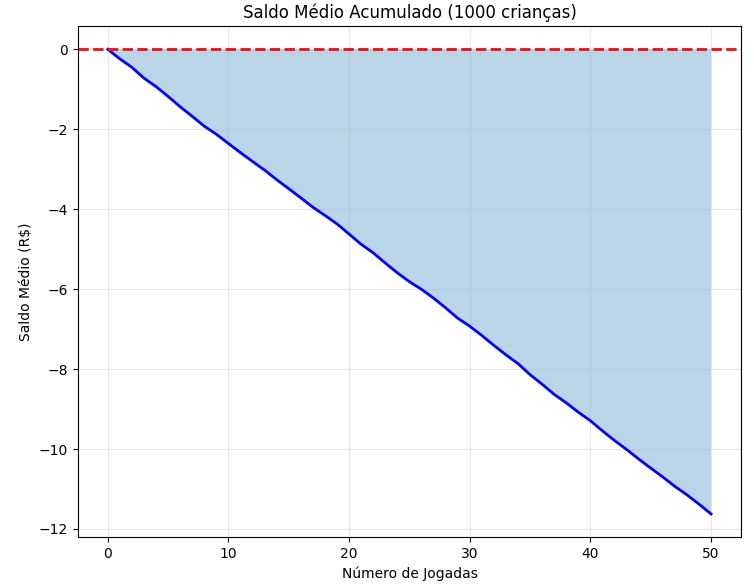
A cada jogada, o(a) Jovem perde em média R$ 0,24

Ou seja:

• Em 10 jogadas: perde uns R$ 2,40

• Em 20 jogadas: perde aproximadamente R$ 4,70

• Em 50 jogadas: perde ~R$ 11,81 (já entra na margem/crédito)

• Em 100 jogadas: perde ~R$ 23,61

Simulação de Monte Carlo

Executando simulação de Monte Carlo...
Simulando 1000 crianças
Cada criança joga 50 vezes

==================================================
RESULTADOS DA SIMULAÇÃO
==================================================
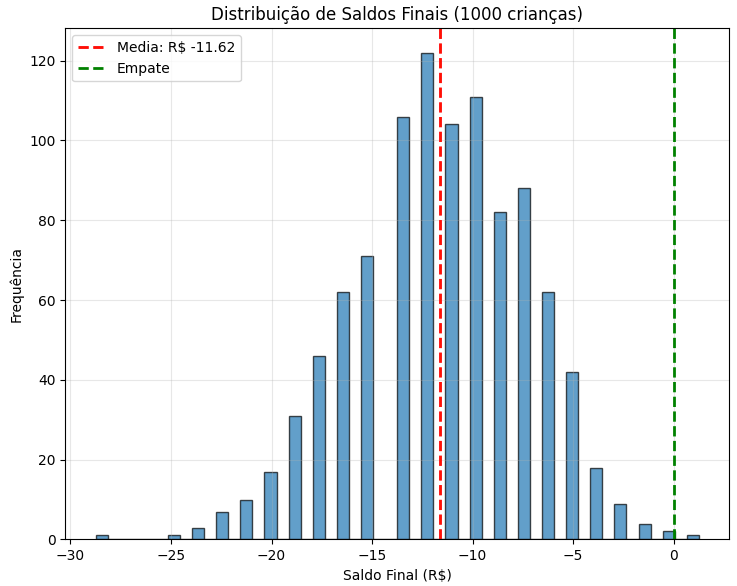
Média de saldo final: R$ -11.62
Mediana de saldo final: R$ -11.25
Desvio padrão: R$ 4.31
Melhor resultado: R$ 1.25
Pior resultado: R$ -28.75

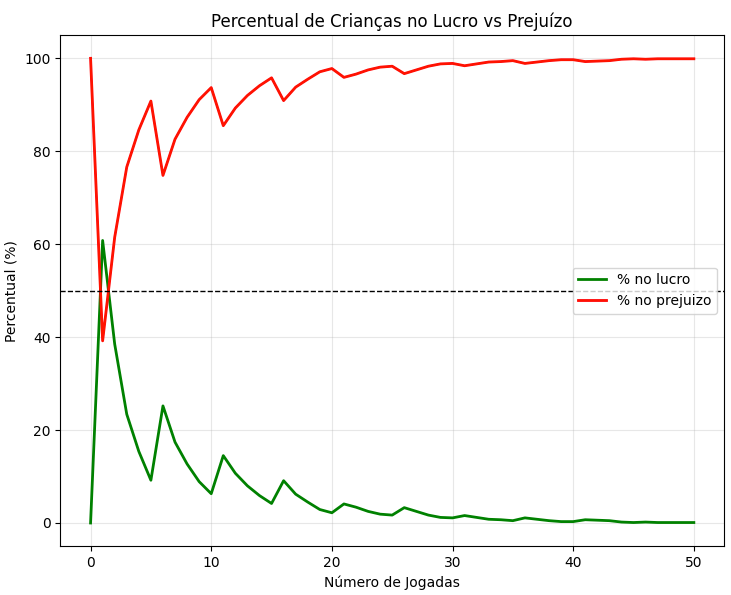
Crianças que ganharam: 1 (0.1%)
Crianças que perderam: 997 (99.7%)
Crianças que empataram: 2 (0.2%)

Expectativa teórica: R$ -11.80
Resultado simulado: R$ -11.62
Diferença: R$ 0.17

Média de DUPLAS MALDITAS em 50 jogadas: 8.4
Probabilidade teórica: 8.3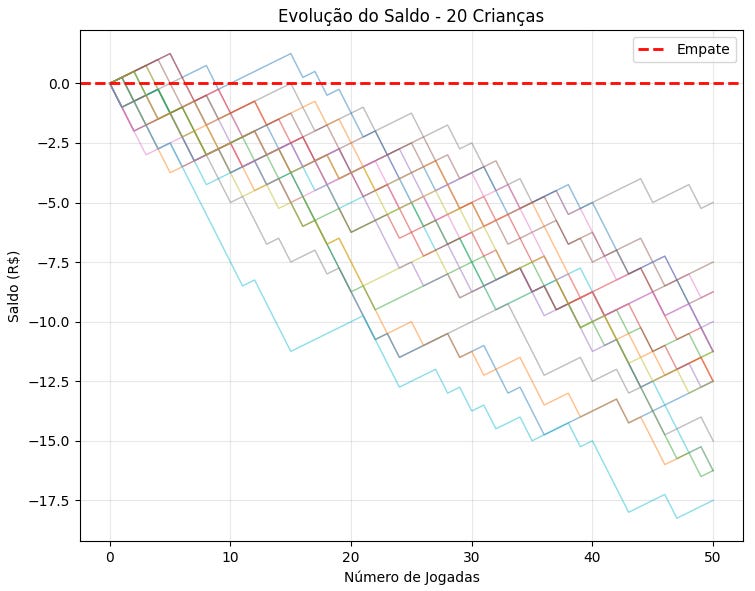

Interpretação do gráfico: a partir da rodada 20, todo o mundo entrou na margem. Na rodada 50, quando a simulação terminou, ninguém conseguiu sair das dívidas nem recuperar o que perdeu.

Interpretação do gráfico: os saldos finais das 1000 crianças negativos para praticamente todos que apostaram. 99,7% perderam para a banca. Aproximadamente 67% terminaram devendo entre -R$ 5 e -R$ 20. Para quem começou o jogo com R$ 5,00, isso apresenta uma alavancagem entre 1 e 4 vezes. A média de alavancagem ficou em 2 vezes.

Interpretação do gráfico: o saldo médio acumulado das 1000 crianças caiu de forma consistente ao longo das 50 rodadas.

Interpretação do gráfico: em poucas jogadas, as crianças perdem tudo o que possuem e operam no prejuízo. Na rodada 40, praticamente todas estão deficitárias.

Vantagem da Banca (House Edge)

Fórmula:

Vantagem da Banca = |Expectativa| / Aposta × 100%

Vantagem = 0,2361 / 1,00 × 100%

Vantagem = 23,61%

A banca tem 23,6% de vantagem sobre o(a) Garoto(a)!

Comparando com jogos reais

• Nosso jogo: 23,6%

• Raspadinha: 20-40%

• Bingo: 10-30%

• Caca-níquel: 2-15%

• Roleta (zero único): 2,7%

• Blackjack (ótimo): 0,5-1%

Nosso jogo se assemelha às raspadinhas, pois é muito desvantajoso para o apostador!

Por que o apostador perde mesmo ganhando a maior parte (61%) das apostas?

Resposta curta: ASSIMETRIA

Quando ganha:

Ganha 22 vezes de 36 (61%)

Lucro total: 22 × R$ 0,25 = R$ 5,50

Quando perde:

Perde 14 vezes de 36 (39%)

Prejuízo total: 14 × R$ 1,00 = R$ 14,00

Resultado líquido em 36 jogadas é o seguinte:

R$ 5,50 - R$ 14,00 = -R$ 8,50

Por jogada: -R$ 8,50 / 36 = -R$ 0,236

Pequenos ganhos frequentes < Grandes perdas raras

Os pequenos ganhos frequentes despertam a vontade no(a) garota de continuar no jogo, pois sente que estava vencendo quase sempre, já que teve sorte em 6 de 10 jogadas e só precisava evitar os duplos, que são eventos raros.

Mas a realidade matemática é muito diferente… Cada vitória vale 1/4 de uma derrota, pois precisa ganhar 4 vezes só para compensar 1 perda. Ele(a) ganha só 1,57 vezes para cada perda (22/14). Em outras palavras, o jogo foi desenhado para ser matematicamente IMPOSSÍVEL lucrar. A assimetria é brutal e as “duplas malditas” pesam 17% para a banca.

Finalmente, a Lei dos Grandes Números ainda pesa sobre o(a) coitado(a), pois quanto mais joga, mais se aproxima da expectativa negativa prevista.

Não adianta o que você faça. A matemática sempre vence.

Onde entra o Trading nisso?

Desculpe. A matemática é um assunto fascinante e acabei me esquecendo…

Jogo de criança e jogo de adulto.

Lições do Jogo

1. Ganhar frequentemente NÃO é ganhar dinheiro: você pode ganhar 6 de cada 10 vezes e ainda quebrar;

2. Duplas malditos = armadilhas: eventos raros podem destruir seu progresso;

3. Prêmios pequenos versus perdas grandes: ganhar R$ 0,25 várias vezes não compensa perder R$ 1,00;

4. Empréstimos pioram tudo: você pode terminar devendo e falido;

5. A casa sempre vence: a matemática garante que a banca lucra sempre no longo prazo.

Por enquanto é isso, pessoal. Um abraço e fiquem longe dos jogos.

Até a próxima!

Rogério